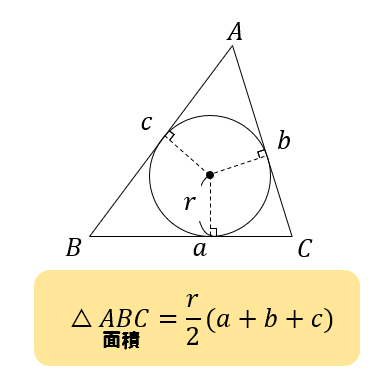
点Dを中心に円を書くと j Dを中心に三角形の3つの辺に接する 円を書くことができます。 この円を 内接円といい、中心を内心といいます。 下の「定理8」は三角形の3つの角の二等分線は1点で交わること の証明ですが、その証明方法をはじめてみる方にとっては、「へぇ~ 垂線か」と思われるかもしれませんが、「角の二等分線」が「各辺から の距離が等しい・「三角形の内角」180°から見て c = 180°(ab) ① ・「直線」(Bl) 180°から見て c = 180° g ② ①=②(c = c)より 180°(ab) = 180° g ab = g g = ab // 「三角形の内角の和」も「直線」も、「どちらも」180°ということを、前回 https//googl/EVb9HF 次回 https//googl/jPrhyo動画のプリント(19ch) http//www19chtv/サブチャンネル とある男が
円に内接する三角形の角度xを求める問題がどうしてもわかりません Yahoo 知恵袋
円 内接 三角形 角度
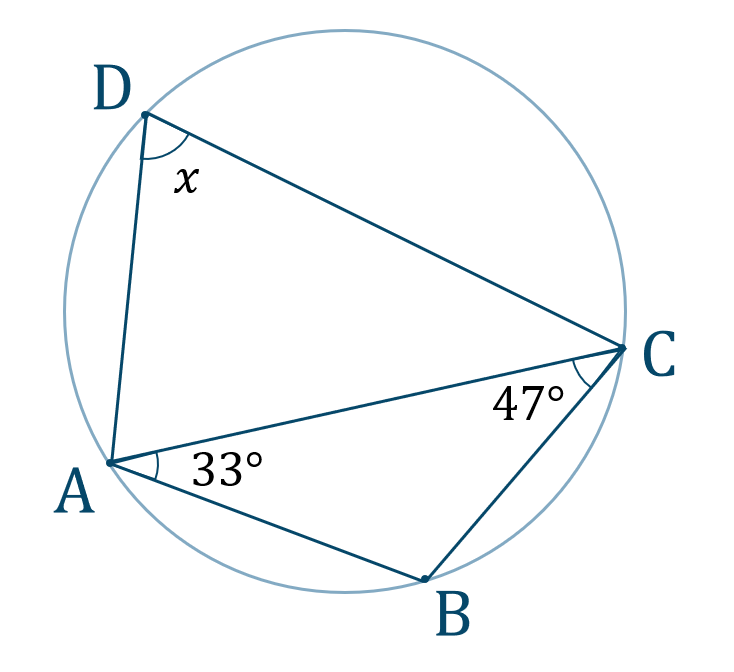
円 内接 三角形 角度- 円や角度に関する作図はこちらもご参考ください(^^) 円の中心を作図する方法とは? 難問円に内接する正三角形の作図方法とは? 角度15°・30°・45°・60°・75°・90°・105°の作り方4 分 秒) (1) {\iac = 35 \iba = 22 a b c i (2) {\ibc = 40 \aib = 117 a b c i (3) \bac = 72 a b c i (4) \bic = 140 a b c i



三角比 内接円の半径の求め方をイチから丁寧にやってみよう 数スタ
S formula (1) S =√s(s−a)(s−b)(s−c), s = (abc) 2 (2) if a≥b,c h = 2S a, B=sin−1 h c, C= sin−1 h b if b≥ c,a h = 2S b, C =sin−1 h a, A=sin−1 h c if c≥ a,b h = 2S c, A= sin−1 h b, B=sin−1 h a (3) ABC三角形は必ず円に内接 する ことを許して、この順序で、角が並ぶような五角形を円に内接 円に内接するn角形を作るには、次式に、p=1、・・・、n を代入した角度で円の中心角360 二等辺三角形の内接円 またまた少しサボってました。 難問を解く力をつけるために,難しい入試問題を数多くといている受験生を見かけます。 塾が宿題をたくさん出すからかもしれません。 多くの入試問題をこなすことは,入試を控える中学生にとっ
A 級2 分30 秒;・「円に内接する四角形の対角の和は180°」定理の証明 もっと見る 円 , 三角形 , 角度 , 弦 , 円の性質 , 円の特徴 ,接円の半径から、3つの二等辺 三角形がある。その底角を図の ようにa,b,c,とすると、 2a+2b+2c=180° 2でわって、 a+b+c=90° b+cーa=90° 外心の角度の関係 その2
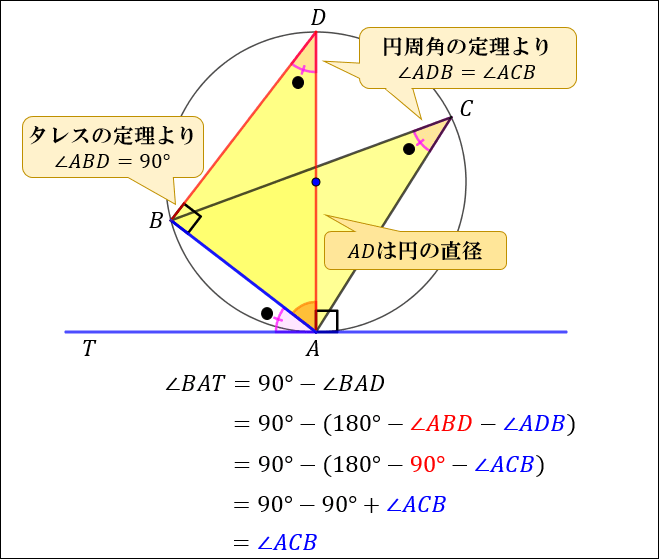
前回 https//wwwyoutubecom/watch?v=G4RJ4fV5k8&index=21&list=PLKRhhk0lEyzOfDE8u9U0GWX3aa43XeMOr 次回 https//wwwyoutubecom/watch?v=hfzt8TVzKBs&indexとなります。また、 は直角三角形なので が得れれます。 2 の場合 下記の図のようになり、半円がつくる円周角は90°なので となります。 3 の場合 下図のように、中心oを通る直線と円との交点をdとします。 円に内接する四角形の対角の和は180°なので 円に内接する四角形の性質まとめ対角の和が180°になる理由 Tooda Yuuto 18年8月22日 / 19年9月9日 四角形の つの頂点 がすべて同じ円周上にある(内側から接している)とき、「四角形 は円に内接する」といいます。 反対に、四角形 の つの辺がすべて




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ
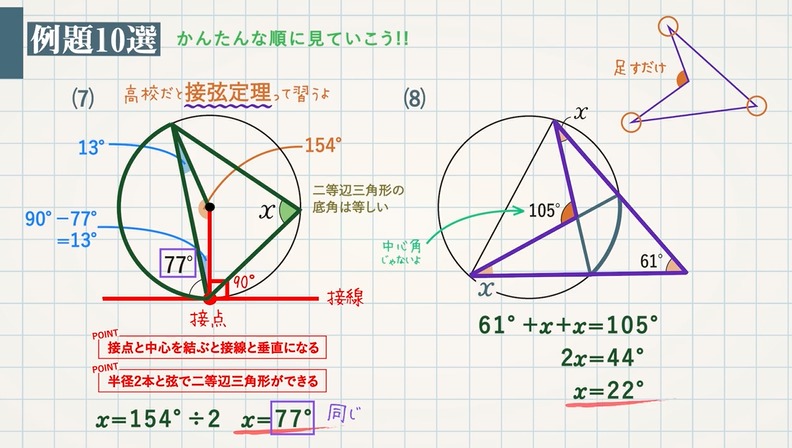



円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
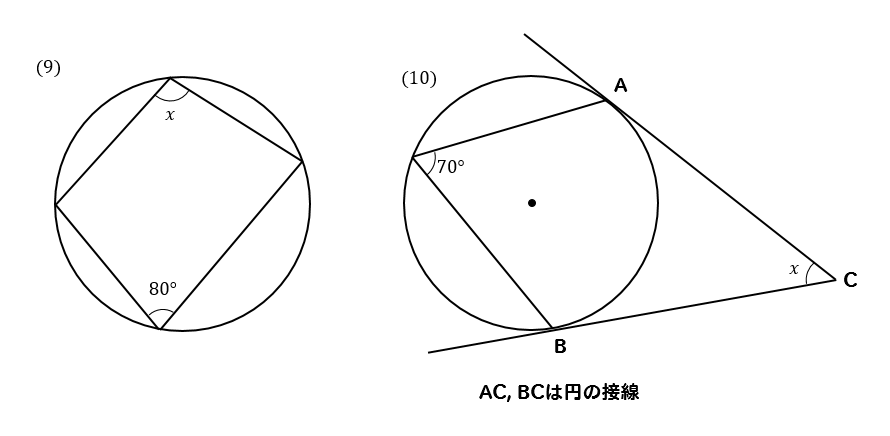
右側の三角形で内角の和は180°だから残り1つの角は70° 次に∠cと70°は円に内接する四角形の向かい合う内角だから∠c70°=180° → ∠c=110°つまり、円に内接する三角形で1°をはさむ2辺の長さが (m,k) のとき、反対側に頂角が60°の三角形を張り合わせて内接四角形を作るとき、その辺の長さの組み合わせ(もちろん無数にあるが)のうち、等脚台形になる (m+k,k) の場合と、(m,m+k) の場合については、七五三三角形同様マークなら暗算で処理してしまいたくなる。 三角形の内接円、外接円、面積、角度 外接円の中心と半径を求めるコードを作ってみました。 公式がわからなかったので、 Wikipedia の外接円の項目を参照しました。 (x1)^2 (y2)^2=3^2という円の方程式の形で結果を出力します。 小数の場合は小数点以下2桁までに四捨五入し、必要のなくなったゼロは消去。 うまく丸める処理が思いつきませんでした。 その



48s96ub7b0z5f Net Naisetsu Shikakukei




角度を求めよう 円とブーメラン 中学数学 Wiki Atwiki アットウィキ
第50問 内接円と外接円 図形ドリル 5年生 6年生 内接円 円 外接円 正方形 ★★★☆☆☆ (中学入試標準レベル) 思わず「お~~! ! 」と言いそうな良問を。 受験算数の定番からマニアックな問題まで。 図形ドリルでは,色々なタイプの図形問題反射テスト 角度 三角形と内接円 01 1 abc の内心をi とする わかる角度全てを図に書きこめ(s 級1 分50 秒; 円 内接 三角形 角度 円 内接 三角形 角度 2月 13, 21 外接円、内接円などは三角比とともに融合されてよく出てきますが、1つひとつ確認していきましょう。 例題1では角度につい



方べきの定理 公式 の覚え方と円に内接する四角形の対角線の性質




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
B 級3 分 秒;円に内接する四角形の対角の和は180°なので� 三角形の内接円とは 三角形の内接円とは、その 三角形の3つの辺すべてに接する円 のことです。 四角形なら4つの辺に接する、五角形なら5つ、といった具合に増えていくのは外接円と同様。 こんにちは。 da Vinch (@mathsouko_vinch)です。 円に内接する四角形とは三角比の分野でよく出てくるのが「円に内接する四角形」です。これは四角形の頂点がすべて円上にあるといってもいいし、四角形の頂点をすべて通るよう



1




三角比 内接円の半径の求め方をイチから丁寧にやってみよう 数スタ
円に内接する三角形の角度xを求める問題がどうしてもわかり ∠abc=90° (aocは直径だから) ∠ocb=∠obc=18° (⊿obcは2等辺三角形だから) x= ∠oba=∠abc∠obc=90°18°=72° こんにちは。三角形の三辺の長さ a,b,c が分かっているとき、三角形の面積Sは、 と表せる。 以下の説明では、左図のように、頂点および角度をa,b,c 内接円 の中心をD入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 女子校 直角三角形 4年生 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 二等辺三角形 直角二等辺三角形 立体の切断 ファイ




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ
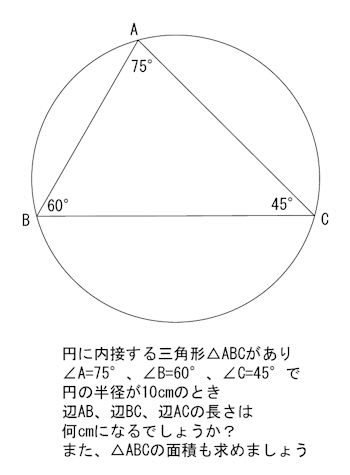



円に内接する 三角形の 問題 名寄 算数数学教室より
三角形の内心 ・ 外心 ・ 重心 三角形の3つの内角の2等分線は、1点で交わり、その点から3辺までの距離は等しい。 この1点で交わった点 I を三角形の内心という。 半径 IL の円が三角形の内接円である。 性質 任意の円は、任意の三つの角度を持つ三角形(もちろん角度の和は 180° に等しい)を内接三角形として持つ。 任意の三角形は適当な円に内接する(そのような円は、その三角形の外接円と呼ばれる)。 接弦定理とは? 接弦定理とは、円に三角形が内接し、その頂点のどれか \(\bf{1}\) 点を通る円の接線があるときに、それらの 角度に関して成り立つ定理 です。



円の中からはみ出ている三角形の問題はどう解けばいいですか 角度x角度yを Yahoo 知恵袋
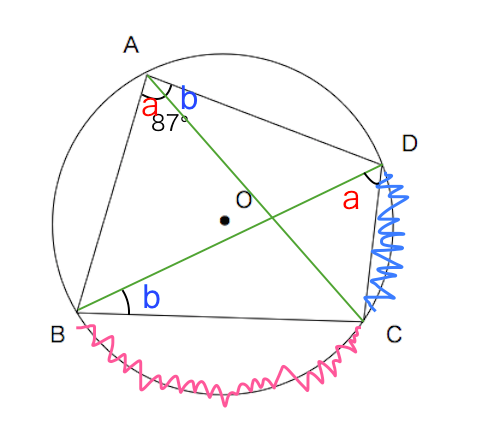



円に内接する四角形 苦手な数学を簡単に
三角形には不思議な性質がたくさんあります。 その中にはまだ発見されていないものもあるはずです。 このジオジェブラを使うと正確な作図が簡単にでき、さらにアニメーションを使って変化を調べることができ、新しい発見が容易にできます。 「bもしかしたら・・・?
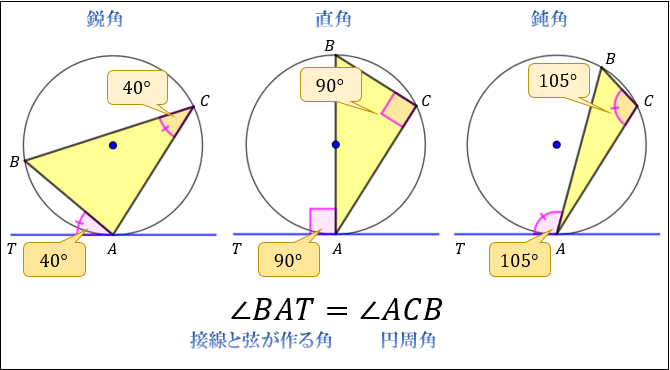



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



外接円 外心について



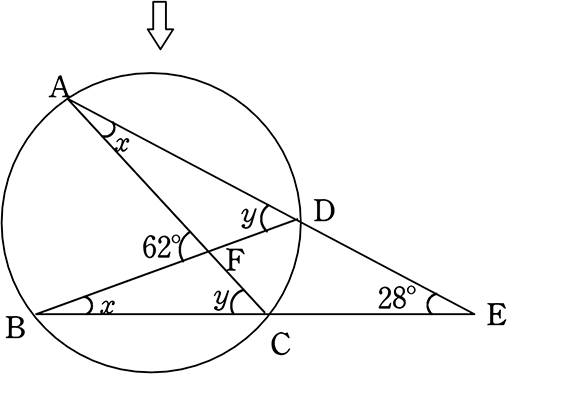
円周角の定理 練習問題 角度がわからない 苦手な数学を簡単に




円に内接する正三角形の問題 社会人になり勉強することもなくなったのですが Okwave



内接円 内心



中学数学 円周角 中心角
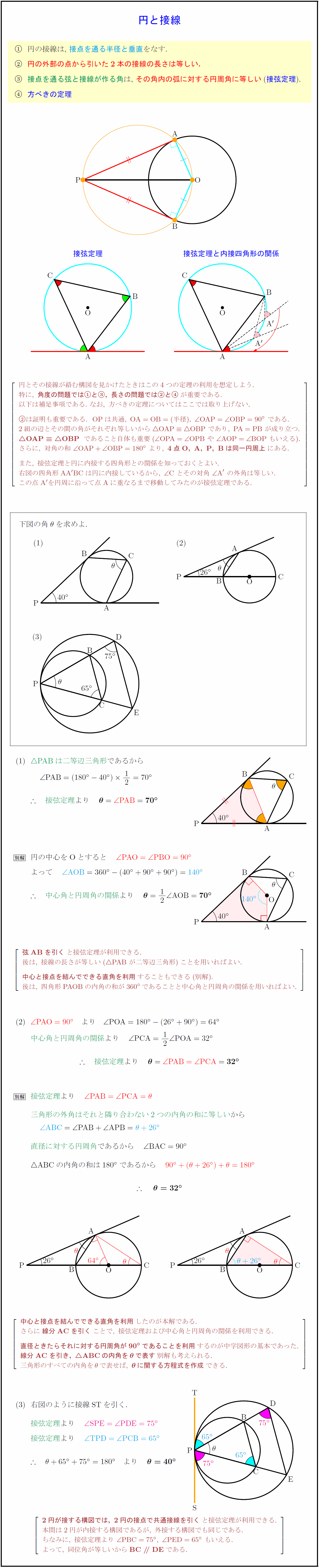



高校数学a 円と接線に関する3定理 垂直 接線の長さ 接弦定理 受験の月




円に内接する四角形の性質 高校数学の知識庫



三角形に内接する相似三角形 Geogebra




高校数学 円に内接する四角形の対角線の長さと面積 受験の月




高校数学 円に内接する四角形の計量 基本と裏技のまとめ トレミーの定理 ブラーマグプタの公式他 受験の月




高校数学a 円周角と中心角のおさらい 例題編 映像授業のtry It トライイット
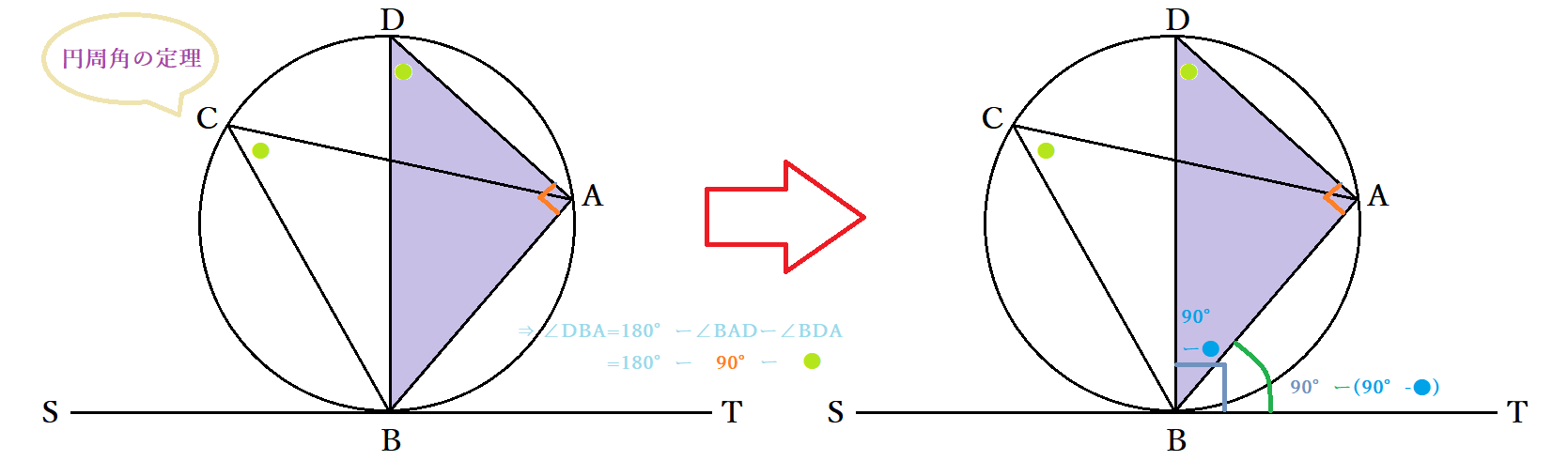



接弦定理とは 接線と弦の作る角の定理の証明 覚え方と応用問題 中学 高校 Curlpingの幸せblog



Aの角度を教えてください 円に内接する四角形の対角の和が180 よ Yahoo 知恵袋
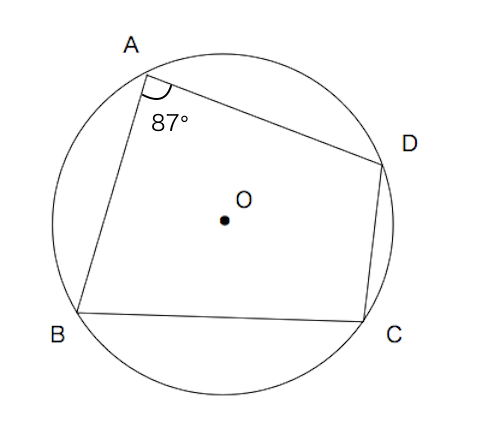



円に内接する四角形 苦手な数学を簡単に




57 円に内接する三角形 と 円に内接する四角形 を比べる とちぎeライブラリ



円と三角形 角度 中学から数学だいすき




勉強しよう数学解答集 三角形の垂心の周りの角度



円と三角形 角度 中学から数学だいすき



円周角の定理 理数系無料オンライン学習 Kori



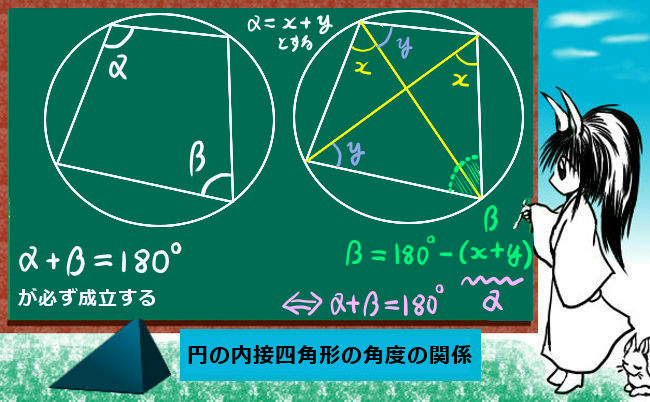
円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ



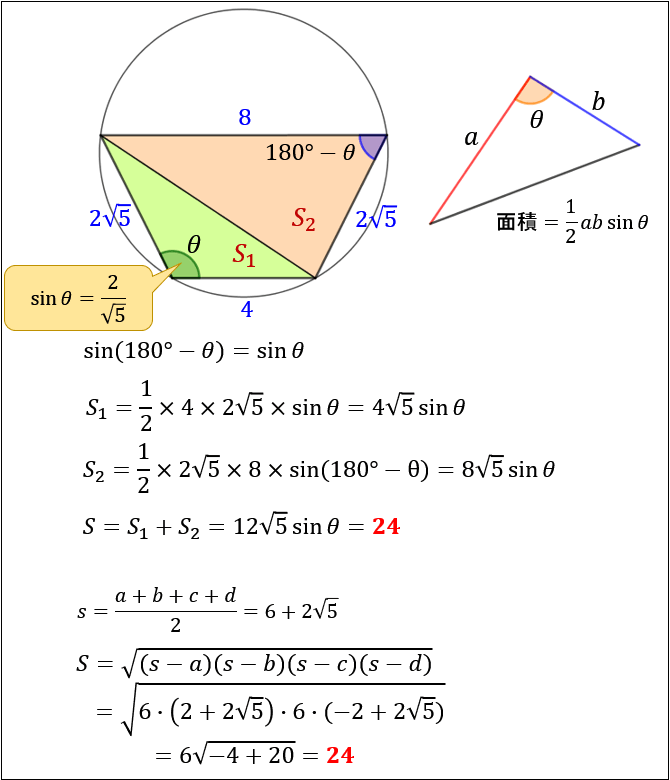
円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室



円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室



七五三 三角形から円に内接する四角形へ



角度 円と四角形 中学から数学だいすき




中3 数学 円に内接する四角形の問題です この問題がわからないので 教 数学 教えて Goo
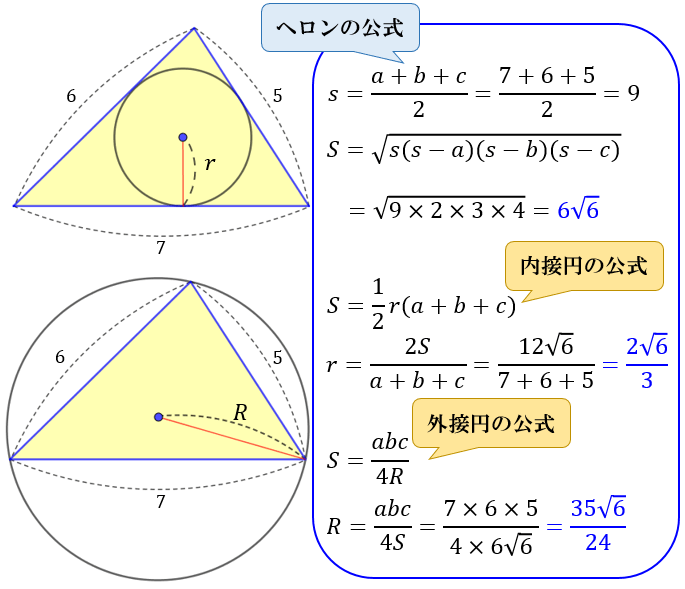



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



内接円 内心




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア



三角形に内接する相似三角形 Geogebra



円に内接する三角形の角度xを求める問題がどうしてもわかりません Yahoo 知恵袋




二等辺三角形の内接円 高校入試 数学の良問を解く




接線と円の関係 Jsciencer




三角形の外接円の 4 つの性質 証明付 理数アラカルト




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




中学数学 円周角 中心角



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典



1



1
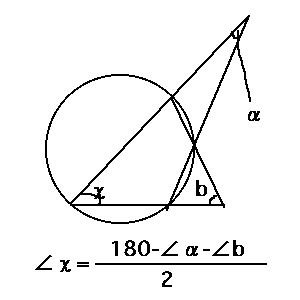



角度を求めよう 円とブーメラン 中学数学 Wiki Atwiki アットウィキ



七五三 三角形から円に内接する四角形へ



七五三 三角形から円に内接する四角形へ
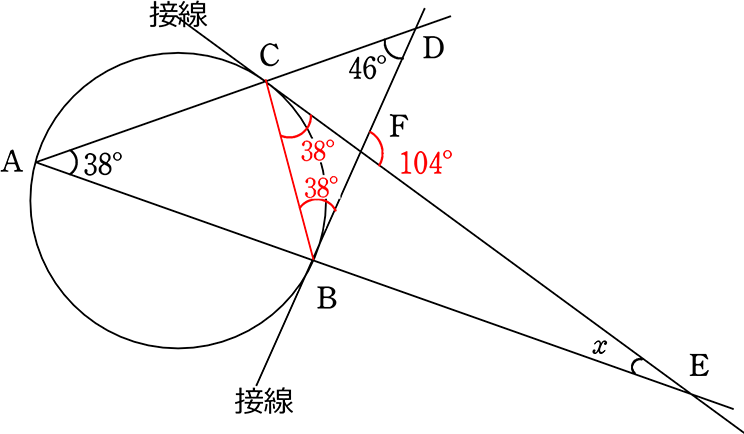



中学数学 円周角 中心角



Math 円 5 直角三角形に内接する円の半径 働きアリ




Xの角度の求め方を教えてください 3 と 5 です 円周角の問題です Clear
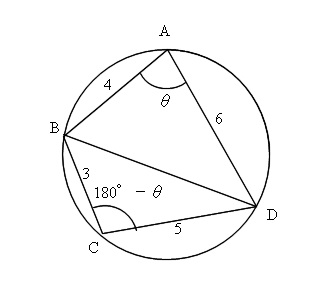



円に内接する四角形の面積の求め方と定理の使い方




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
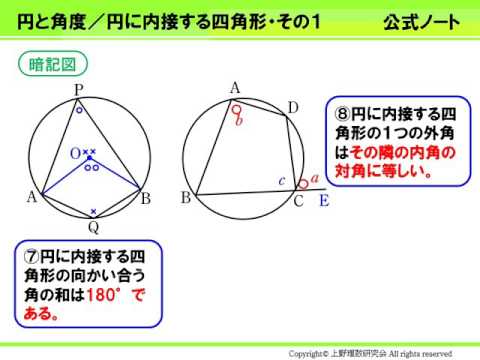



円と角度04 内接四角形の性質 Youtube




円に内接する三角形について 次の問題がわかりません 教えていただ 数学 教えて Goo
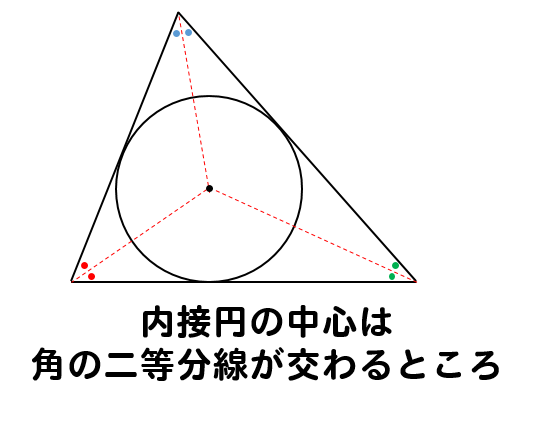



作図 三角形の内接円 外接円のかき方をポイント解説 数スタ



数学a 円に内接する四角形と角の使い方とコツ 教科書より詳しい高校数学



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ



Math 三角形に内接する円 働きアリ




中学数学 円の中の三角形の角度の問題 お世話になります 円の中の三角形 Okwave




円周角の定理 角度の計算方法と中心角 弧の長さの関係 リョースケ大学



円周角



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
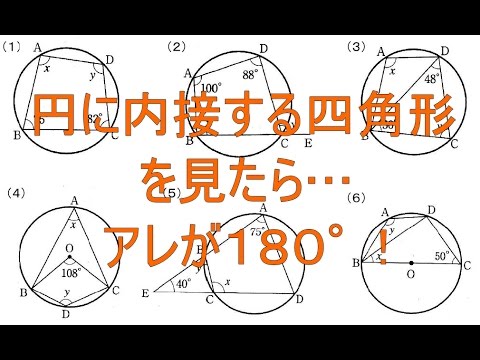



円に内接する四角形の性質 中学3年数学 Youtube




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ
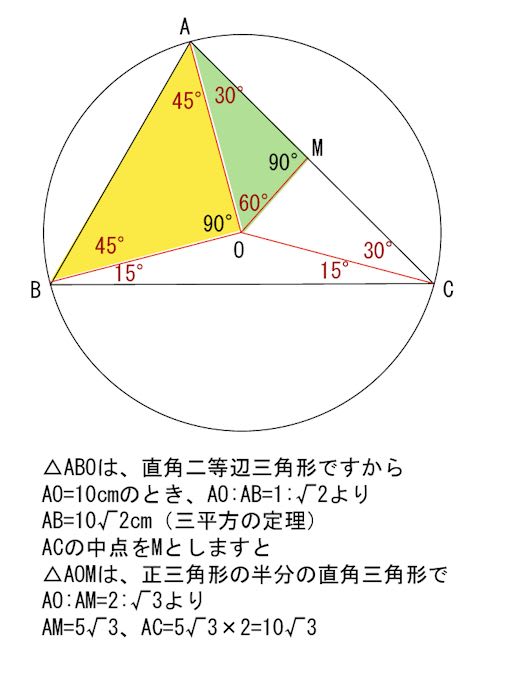



円に内接する 三角形の 問題 3 名寄 算数数学教室より



Excel Vba 数学実験室 正三角形と内接する円の面積比
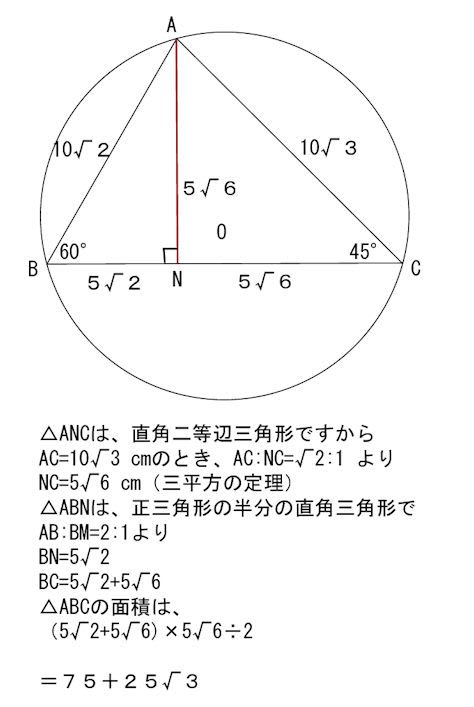



円に内接する 三角形の 問題 4 名寄 算数数学教室より
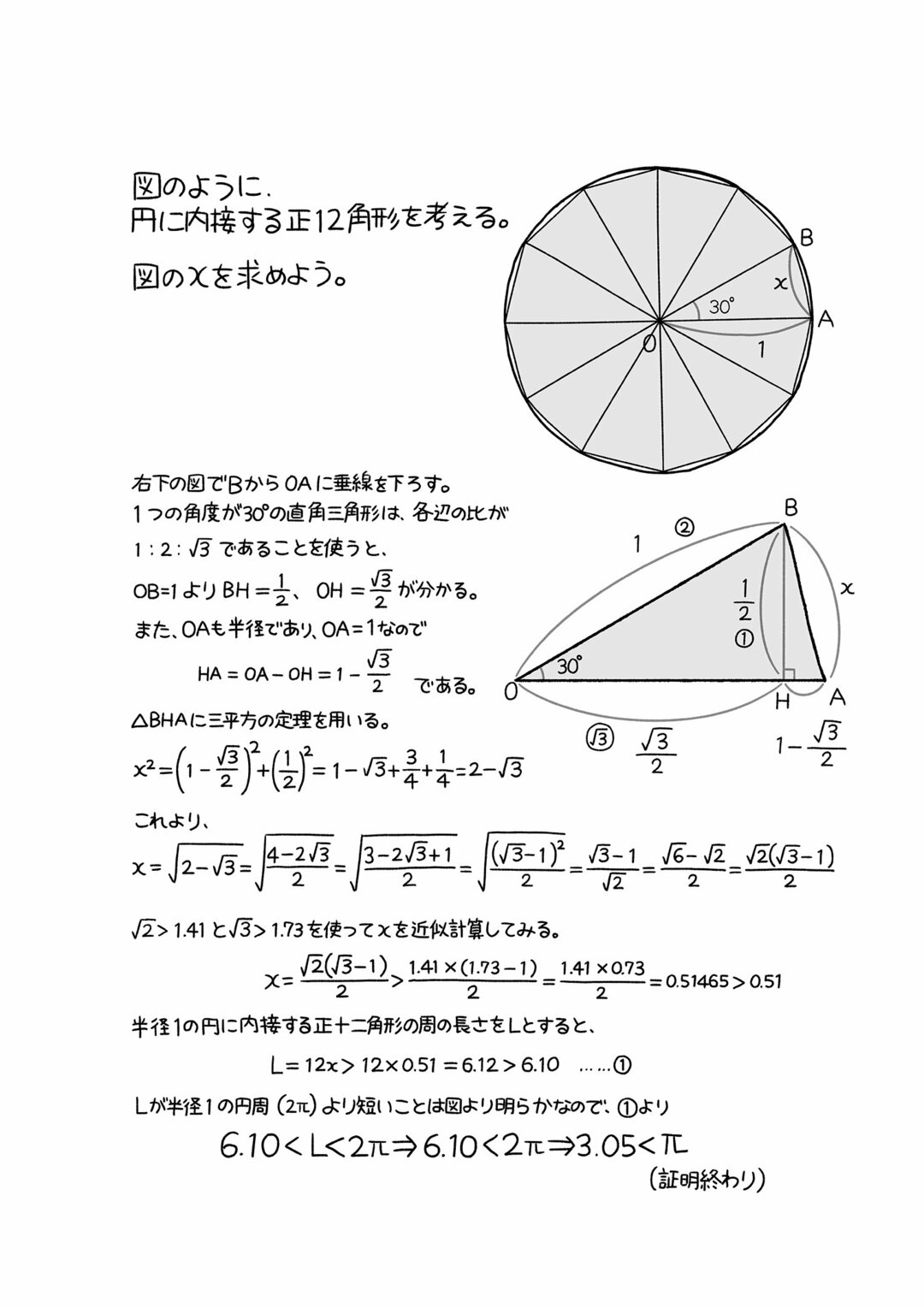



東大入試の有名問題 から円周率を探求する とてつもない数学 ダイヤモンド オンライン




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ
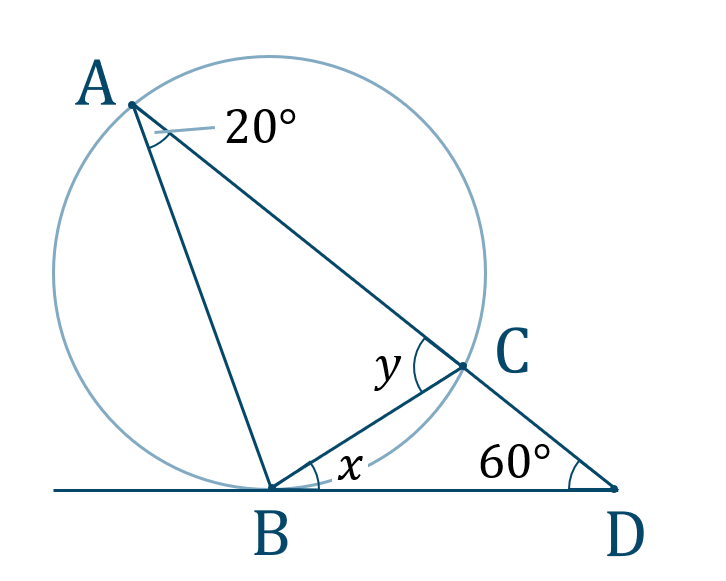



数学a 接弦定理の使い方とコツ 教科書より詳しい高校数学
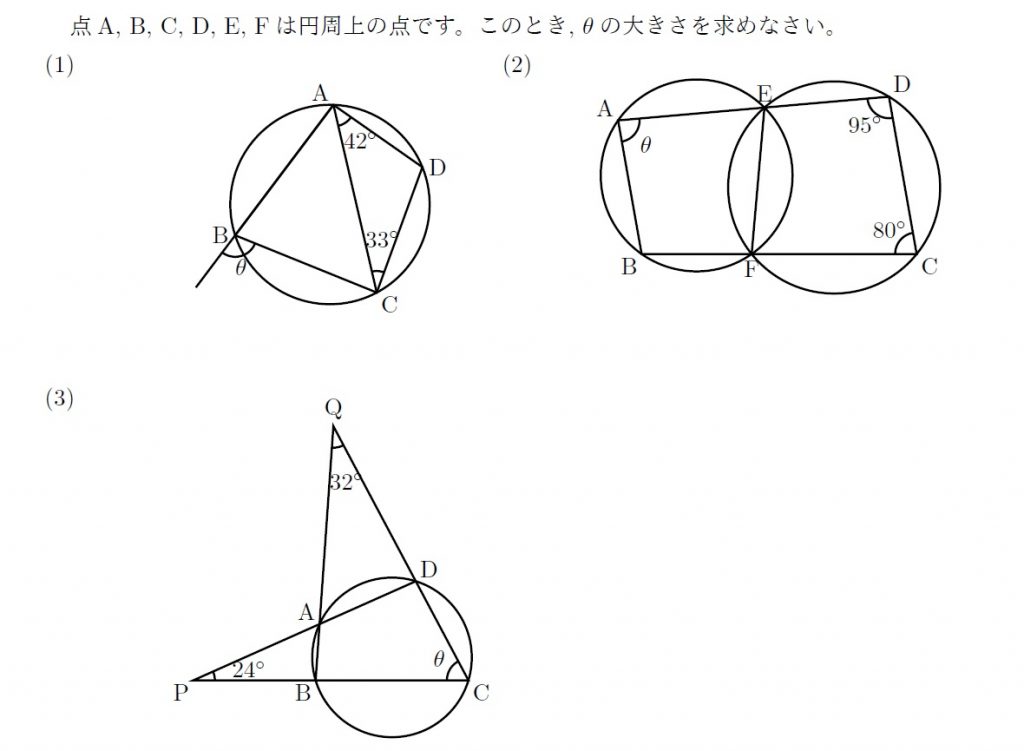



Emathソースコード 円に内接する四角形と角度 数樂管理人のブログ
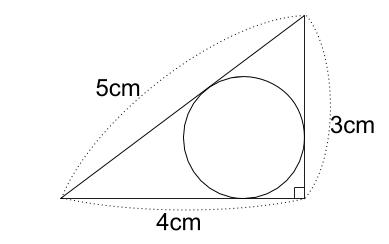



三角形の内接円 中学数学の無料オンライン学習サイトchu Su




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




円に関する性質その1 接弦定理 高校数学の知識庫




高校数学 数 96 円に内接する四角形 Youtube
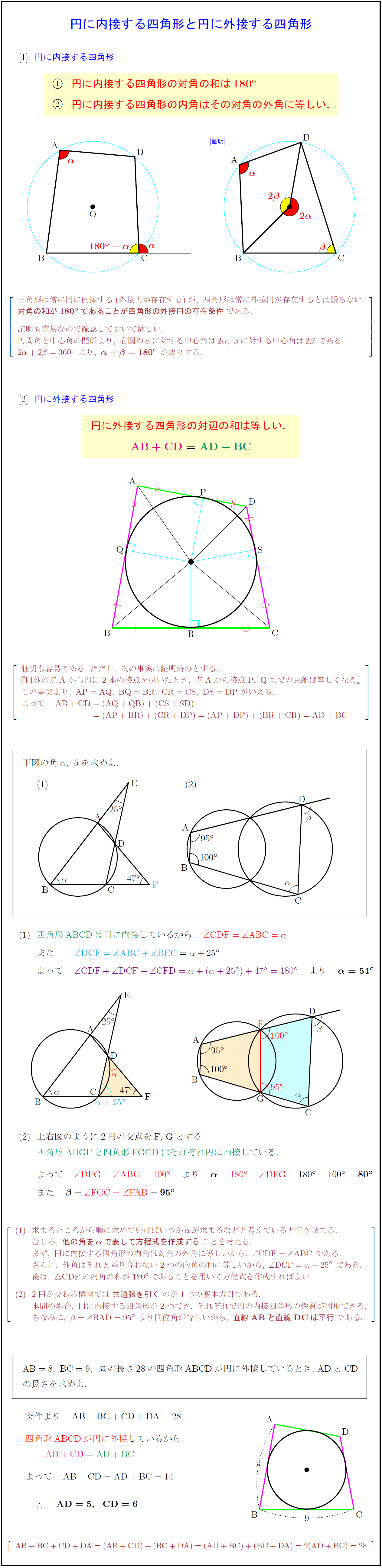



高校数学a 円に内接する四角形と円に外接する四角形の性質の証明 受験の月
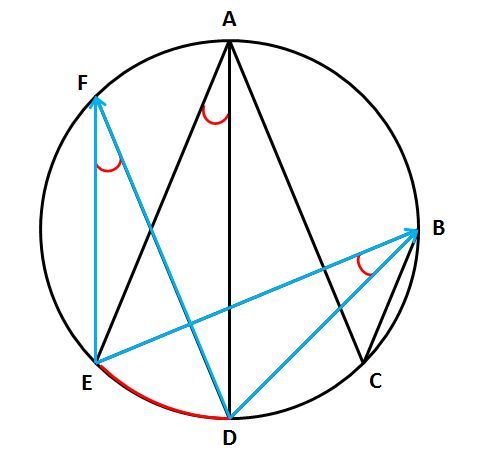



円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
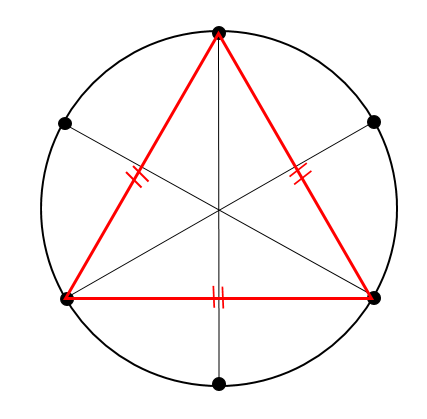



作図 円に内接する正三角形の作図方法とは 数スタ
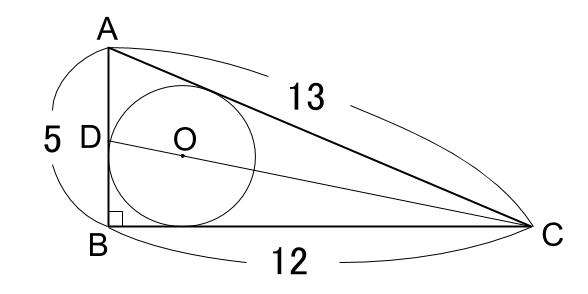



内接円と角の2等分 中学数学の無料オンライン学習サイトchu Su




Math 円 5 直角三角形に内接する円の半径 働きアリ




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




円に内接する四角形 Jsciencer



円に内接する二等辺三角形 駒場東邦中学 04年 パズル おもしろ算数問題



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典



1



円に内接する四角形
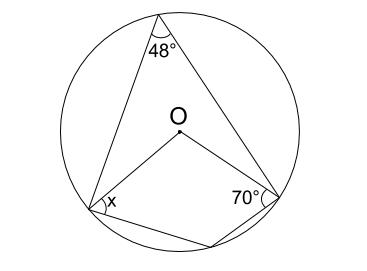



円に内接する四角形の性質 中学数学の無料オンライン学習サイトchu Su




標準 三角比と円に内接する四角形 なかけんの数学ノート




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




接線の性質 なぜこの記号同士が同じ角度になるのかが分かりません Clear
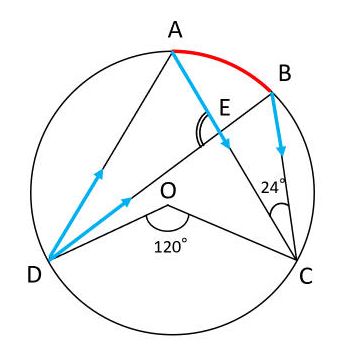



円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室



0 件のコメント:
コメントを投稿